Multi-Core By Default
On multi-core programming, not as a special-case technique, but as a new dimension in all code.
Learning to program a single CPU core is difficult. There is an enormous number of techniques, amount of information, and number of hours to spend in order to learn to do it effectively. Learning to program multiple CPU cores to do work in parallel, all while these cores cooperate in accomplishing some overarching task, to me seemed like the anvil that broke the camel’s back—so to speak—there is already so much to wrangle when doing single-core programming, that for me, it was much more convenient to ignore multi-core programming for a long time.
But in the modern computer hardware era, there emerges an elephant in the room. With modern CPU core counts far exceeding 1—and instead reaching numbers like 8, 16, 32, 64—programmers leave an enormous amount of performance on the table by ignoring the fundamentally multi-core reality of their machines.
I’m not a “performance programmer”. Like Casey Muratori (which is partly what made me follow him to begin with), I have always wanted reasonable performance (though this might appear like “performance programming” to a concerning proportion of the software industry), but historically I’ve worked in domains where I control the data involved, like my own games and engines, where I am either doing the art, design, and levels myself, or heavily involved in the process. Thus, I’ve often been able to use my own programming constraints to inform artistic constraints.
All of that went out the window over the past few years, when in my work on debuggers, I’ve needed to work with data which is not only not under my control, but is almost exactly identical to the opposite of what I’d want—it’s dramatically bigger, unfathomably poorly structured, extraordinarily complicated, and not to mention unpredictable and highly variable. This is because, as I’ve written about, debuggers are at a “busy intersection”. They deal with unknowns from the external computing world on almost all fronts. And if one wanted a debugger to be useful for—for instance—extraordinarily large codebases that highly successful companies use to ship real things, those unknowns include unfortunate details about those codebases too.
As such, in my work, making more effective use of the hardware has been far more important than it ever has been for me in the past. As such, I was forced to address the “elephant in the room” that is CPU core counts, and actually doing multi-core programming.
I’ve learned a lot about the multi-core aspect of programming in the past few years, and I’ve written about lessons I’ve learned during that time, like those on basic mental building blocks I used to plan for multithreaded architecture, and carefully organizing mutations such that multiple threads require little-to-no synchronization.
I still find those ideas useful, and my past writing still captures my thoughts on the first principles of multi-core programming. But recently, thanks to some lessons I learned after a few discussions with Casey, my abilities in concretely applying those first principles have “leveled up”. I’m writing this post now to capture and share those lessons.
The Parallel for (And Its Flaws)
Because every programmer learns single-core programming first, it’s common—after one first learns multi-core programming techniques—to apply those techniques conservatively within otherwise single-core code.
To make this more concrete, consider the following simple example:
S64 *values = ...;
S64 values_count = ...;
S64 sum = 0;
for(S64 idx = 0; idx < values_count; idx += 1)
{
sum += values[idx];
}In this example, we compute a sum of all elements in the values array. Let’s now consider a few properties of sums:
a + b + c + d = (a + b) + (c + d)a + b + c + d = d + c + b + a(a + b) + (c + d) = (c + d) + (a + b)
Because we can reconsider a sum of elements as a sum of sums of groups of those elements, and because the order in which we sum elements does not impact the final computation, the original code can be rewritten like:
S64 *values = ...;
S64 values_count = ...;
S64 sum0 = 0;
for(S64 idx = 0; idx < values_count/4; idx += 1)
{
sum0 += values[idx];
}
S64 sum1 = 0;
for(S64 idx = values_count/4; idx < (2*values_count)/4; idx += 1)
{
sum1 += values[idx];
}
S64 sum2 = 0;
for(S64 idx = (2*values_count)/4; idx < (3*values_count)/4; idx += 1)
{
sum2 += values[idx];
}
S64 sum3 = 0;
for(S64 idx = (3*values_count)/4; idx < (4*values_count)/4 && idx < values_count; idx += 1)
{
sum3 += values[idx];
}
S64 sum = sum0 + sum1 + sum2 + sum3;That obviously doesn’t win us anything—but what this means is that we can obtain the same result by subdividing the computation into several, smaller, independent computations.
Because several independent computations do not require writing to the same memory, they fit nicely with multi-core programming—each core does not need to synchronize at all with any other. This not only greatly simplifies the multi-core programming, but improves its performance—or, more precisely, it doesn’t eat away from the natural performance obtained by executing in parallel.
For cases like this, we can implement what’s known as a “parallel for”. The idea is that we’d like to specify our original for loop…
for(S64 idx = 0; idx < values_count; idx += 1)
{
sum += values[idx];
}…but we’d like to also express that the loop can be subdivided into independent computations (the results of which we can join into a single result later).
In other words, we begin with normal, single-core code. But, for some computation, we want to “go wide”, and compute something in parallel. Then, we want to “join” this wide, parallel work, and go back to more single-core code, which can use the results of the work done in parallel.
This is a widely known and used concept. In many real codebases written in modern programming languages which offer many tools for abstraction building, you’ll find a number of impressive gymnastics to succinctly express this.
One of the reasons I prefer working in a simpler language is that, if what my code ultimately generates to facilitate some abstraction is complicated, that being reflected directly in the source code helps keep me honest about how “clean” some construct actually is.
If, on the other hand, some higher level utility can be provided by a simple and straightforward concrete implementation, that is a sign of a superior design—one that does not compromise on its implementation, but also does not compromise on its higher level utility.
Many people behave as though this is impossible—that higher level utility necessarily incurs substantial tradeoffs at the low level, or vice versa, that low level properties like performance necessitate undesirable high level design. This is simply not universally true. By hunting for tradeoffs, many programmers train themselves to ignore cases when they can both have, and eat, their cake.
So, if we consider our options for implementing a “parallel for” without a lot of modern language machinery, we might start with something like this:
struct SumParams
{
S64 *values;
S64 count;
S64 sum;
};
void SumTask(SumParams *p)
{
for(S64 idx = 0; idx < p->count; idx += 1)
{
p->sum += p->values[idx];
}
}
S64 ComputeSum(S64 *values, S64 count)
{
S64 count_per_core = count / NUMBER_OF_CORES;
SumParams params[NUMBER_OF_CORES] = {0};
Thread threads[NUMBER_OF_CORES] = {0};
for(S64 core_idx = 0; core_idx < NUMBER_OF_CORES; core_idx += 1)
{
params[core_idx].values = values + core_idx*count_per_core;
params[core_idx].count = count_per_core;
S64 overkill = ((core_idx+1)*count_per_core - count);
if(overkill > 0)
{
params[core_idx].count -= overkill;
}
threads[core_idx] = LaunchThread(SumTask, ¶ms[core_idx]);
}
S64 sum = 0;
for(S64 core_idx = 0; core_idx < NUMBER_OF_CORES; core_idx += 1)
{
JoinThread(threads[core_idx]);
sum += params[core_idx].sum;
}
return sum;
}There are a number of unfortunate realities about this mechanism:
In something like
LaunchThreadandJoinThread, we interact with the kernel to create and destroy kernel resources (threads) every time we perform a sum.The actual case-specific code we needed (for the sum, in this case), and the number of particular details we had to specify and get right—like the work subdivision—has exploded. What used to be a simple
forloop has been spread around to different, more intricate parts, all implementing different details of the mechanism we wanted—the work preparation, the work kickoff, and the joining and combination of work results. All parts must be maintained and changed together, every time we want a parallelfor.The solution’s control flow has been scattered across threads, CPU cores, and time. We can no longer trivially step through the sum in a debugger. If we encounter a bug in some iterations in a parallel
for, we need to correlate the launching of that particular work, and that actual work. For example, if we stop the program in the debugger and find ourselves within a thread performing some iterations of the parallelfor, we have lost context about who launched that work (in single-core code, this information is universally provided with call stacks).
The first problem can be partly addressed with a new underlying layer which our code uses instead of the underlying kernel primitives. In many codebases, this layer is called a “job system”, or a “worker thread pool”. In those cases, the program prepares a set of threads once, and these threads simply wait for work, and execute it once they receive it:
void JobThread(void *p)
{
for(;;)
{
Job job = GetNextJob(...);
job.Function(job.params);
}
}
void SumJob(SumParams *p)
{
...
}
S64 ComputeSum(S64 *values, S64 count)
{
Job jobs[NUMBER_OF_CORES] = {0};
for(S64 core_idx = 0; core_idx < NUMBER_OF_CORES; core_idx += 1)
{
...
jobs[core_idx] = LaunchJob(SumJob, ¶ms[core_idx]);
}
S64 sum = 0;
for(S64 core_idx = 0; core_idx < NUMBER_OF_CORES; core_idx += 1)
{
WaitForJob(jobs[core_idx]);
sum += params[core_idx].sum;
}
return sum;
}In this case, there is still some overhead incurred by sending to and receiving information from the job threads, but it is significantly lighter than interacting with the kernel.
But it hasn’t improved the higher level code very much at all—we’ve simply replaced “threads” with “jobs”. The latter two problems hold. We still need to perform an entire dance in order to set up a “wide loop”—a “parallel for”, which scatters control flow for a problem across both source code, and coherent contexts (CPU cores, call stacks) at runtime.
In this concrete case—computing a sum in parallel—this is not a huge concern. Will it compute a sum in parallel? Yes. Does it have very few shared data writes? Yes. Can you parallelize all similarly parallelizable problems this way? Yes. But, we pay the costs of these problems every time we use this mechanism. If we have to pay that cost very frequently throughout a problem, it can become onerous to write, debug, and maintain all of this machinery.
The Job System (And Its Flaws)
One desirable property of the parallel for is that all jobs—which execute at roughly the same time, across some number of cores—are identical in their “shape”. Each job thread participating in the problem is executing exactly the same code—we simply parameterize each job slightly differently, to distribute different subproblems to different cores. This makes understanding, predicting, profiling, and debugging such code much simpler.
Furthermore, within a parallel for, each job’s lifetime is scoped by the originating single-core code’s lifetime. Each job begins and ends within some scope—the scope responsible for launching, then joining, all of the jobs. This means no substantial lifetime management complexity occurs—allocations for a parallel for are as simple as for normal single-core code.
But in practice, the mechanism often used to implement parallel fors—the job system—is rarely only used in this way, which is understandable, given its highly generic structure. For example, it’s also often used to launch a number of heterogeneous jobs. In these cases, it becomes even more difficult to understand the context of a particular job—who launched it, and in what context? It also becomes more difficult to comprehensively understand a system—because there is such a large number of possible configurations of thread states, it can be difficult to ensure a threaded system is robust in all cases.
These jobs are also often not bounded by their launcher scope—as such, more engineering must be spent on managing resources, like memory allocations, whose lifetimes are now defined by what happens across multiple threads in multiple contexts.
And this is, really, the tip of the iceberg. In more sophisticated systems, one might observe that there are dependencies between jobs, and jobs ought to be implicitly launched when their dependency jobs complete, creating an even longer (and more difficult to inspect) chain of context related to some independent through line of work.
Ultimately, this presents recurring writing, reading, debugging, and maintenance costs that don’t exist in normal single-core code. All of the costs incurred by this job system design—whether used in a parallel for or otherwise—are paid any time new parallel work is introduced, or any time parallel work is maintained.
Now, if we have few parts of our code that can be parallelized in this way, then this is not a significant cost.
…But that if is doing a lot of heavy lifting.
In practice, I’ve found that an enormous number of systems are riddled with opportunities for parallelization, because of a lack of serial dependence between many of their parts. But, if taking advantage of every instance of serial independence requires significantly more engineering than just accepting single-core performance, then in many cases, programmers will opt for the latter.
Again—does this mean that a job system cannot be used to do such parallelization in these systems? No. But, it also means that we pay the costs of using this job system—the more moving parts; the extra code and concepts to write, read, and debug—much more frequently, if we’d like to take advantage of this widespread serial independence, or if we’d like any algorithm in particular to scale its performance with the number of cores.
Single-Core By Default
The critical insight I learned from speaking with Casey on this topic was that a significant reason why these costs arise is because of the careful organization a system needs in order to switch from single-core to multi-core code. Mechanisms like job systems and their special case usage in parallel fors represent, in some sense, the most conservative application of multi-core code. The vast majority of code is written as single-core, and a few carveouts are made when multi-core is critically important. In other words, code remains single-core by default, and in a few special cases, work is done to briefly hand work off to a multi-core system.
Because the context of code execution changes across time—because work is handed off from one system to another—it necessarily requires more code to set up, and it is more difficult to debug and understand the full context at any point in time.
But is this the best approach? Perhaps, instead of writing single-core code (which sometimes goes wide) by default, we can write multi-core code (which sometimes goes narrow) by default.
What does this look like in practice?
There’s a good chance that you’ve already experienced this style in other areas of programming—notably, in GPU shader programming.
GPU shaders—like vertex or pixel shaders, used in a traditional GPU rendering pipeline—are written such that they are multi-core by default. You author a single function (the entry point of the shader), but this function is executed on many cores, always, implicitly. The language constructs and rules are arranged in such a way that data reads and writes are always scoped by whatever core happens to be executing the code. A single execution of a vertex shader is scoped to a vertex—a pixel shader to a pixel—and so on.
Because the fundamental, underlying architecture is always multi-core by default, and because there is little involvement of each specific shader in how the multi-core parallelism is achieved, GPU programming enjoys enormous performance benefits, and yet as the shader programmer, it feels that there are few costs to pay for it. So few, in fact, that it feels more like artistic scripting, to the degree that someone can build an entire website—Shadertoy—built around rapid-iteration, high-performance, visual GPU scripting.
Wait a minute… “high performance”, “rapid-iteration scripting”? It seems like many believe that these are mutually exclusive!
Why does CPU programming feel so different?
Contrast the GPU programming model to the usual CPU programming model—you author a single function (the entry point of your program), which is scheduled onto a single core only, normally by a kernel scheduler, using a single thread state. This model is, in contrast, single-core by default.
Long story short: it doesn’t have to be!
Multi-Core By Default
Let’s begin by exactly inverting the approach. Instead of having a single thread which kicks off work to many threads, let’s just have many threads, all running the same code, by default. In a sense, let’s have just one big parallel for:
void BootstrapEntryPoint(void)
{
Thread threads[NUMBER_OF_CORES] = {0};
for(S64 thread_idx = 0; thread_idx < NUMBER_OF_CORES; thread_idx += 1)
{
threads[thread_idx] = LaunchThread(EntryPoint, (void *)thread_idx);
}
for(S64 thread_idx = 0; thread_idx < NUMBER_OF_CORES; thread_idx += 1)
{
JoinThread(threads[thread_idx]);
}
}
void EntryPoint(void *params)
{
S64 thread_idx = (S64)params;
// program's actual work occurs here!
}To click into an architecture which assumes a single-threaded entry point, we start with a BootstrapEntryPoint. But the only work this function actually does is launch all of the threads executing the actual entry point, EntryPoint.
Let’s consider the earlier summation example. First, let’s just take the original single-threaded code, and put it into EntryPoint, and see how we can continue from there.
void EntryPoint(void *params)
{
S64 thread_idx = (S64)params;
// we obtain these somehow:
S64 *values = ...;
S64 values_count = ...;
// compute the sum
S64 sum = 0;
for(S64 idx = 0; idx < values_count; idx += 1)
{
sum += values[idx];
}
}What is actually happening? Well, we’re “computing the sum across many cores”. That is… technically true! Ship it!
There’s just one little problem… This is just as fast as the single-core version, except it also uses enormously more energy, and steals time from other tasks the CPU could be doing, because it is simply duplicating all work on each core.
But, if we were to measure this, and consider the real costs, and profile the actual code, the profile would look something like this:
Duplication itself is not, in principle, a problem, and it is sometimes not to be avoided, because deduplication can sometimes be more expensive than duplication. For instance, communicating the result of a single add instruction across many threads—to deduplicate the work of that add—would be vastly more expensive than simply duplicating the add itself. We do want deduplication, but only when necessary, or when it actually helps.
So, where does it help? Unsurprisingly in this case, the dominating cost—the reason we are using multiple cores at all—is the sum across all elements in values. We want to distribute different parts of the sum across cores. To start, instead of computing the full sum, we can instead compute a per-thread sum. After each per-thread sum is computed, we can then combine them:
void EntryPoint(void *params)
{
S64 thread_idx = (S64)params;
// we obtain these somehow:
S64 *values = ...;
S64 values_count = ...;
// decide this thread's subset of the sum
S64 thread_first_value_idx = ???;
S64 thread_opl_value_idx = ???; // one past last
// compute the thread sum
S64 thread_sum = 0;
for(S64 idx = thread_first_value_idx;
idx < thread_opl_value_idx;
idx += 1)
{
thread_sum += values[idx];
}
// combine the thread sums
S64 sum = ???;
}We have two blanks to fill in:
How do we decide each thread’s subset of work?
How do we combine all thread sums?
Let’s tackle each.
1. Deciding Per-Thread Work
Currently, the only input I’ve provided each thread is its index, which would be in [0, N), where N is the number of threads. This is stored in the local variable thread_idx, which will have a different value in [0, N) for each thread. This is an easy example, because a good way to distribute the sum work across all threads is to uniformly distribute the number of values to sum amongst the threads. This means we are simply mapping [0, M) to [0, N), where M is the number of values—values_count—and N is the number of threads.
We can almost compute this as follows:
S64 values_count = ...;
S64 thread_idx = ...;
S64 thread_count = NUMBER_OF_CORES;
S64 values_per_thread = values_count / thread_count;
S64 thread_first_value_idx = values_per_thread * thread_idx;
S64 thread_opl_value_idx = thread_first_value_idx + values_per_thread;This is almost right, but only almost, because we also need to account for the case where values_count is not cleanly subdivided by thread_count. Because our values_per_thread will truncate to the next lowest integer, this current distribution will underestimate the number of values we need to compute per thread, by anywhere from 0 (if it divides cleanly) to thread_count-1 values—or in other words, the remainder of the division.
Thus, the number of values this division underestimates by—the “leftovers”—can be computed as follows:
S64 leftover_values_count = values_count % thread_count;We can then distribute these leftovers amongst the first leftover_values_count threads:
// compute the values-per-thread, & number of leftovers
S64 values_per_thread = values_count / thread_count;
S64 leftover_values_count = values_count % thread_count;
// determine if the current thread gets a leftover
// (we distribute them amongst the first threads in the group)
B32 thread_has_leftover = (thread_idx < leftover_values_count);
// decide on how many leftovers have been distributed before this
// thread's range (just the thread index, clamped by the number of
// leftovers)
S64 leftovers_before_this_thread_idx = 0;
if(thread_has_leftover)
{
leftovers_before_this_thread_idx = thread_idx;
}
else
{
leftovers_before_this_thread_idx = leftover_values_count;
}
// decide on the [first, opl) range:
// we shift `first` by the number of leftovers we've placed earlier,
// and we shift `opl` by 1 if we have a leftover.
S64 thread_first_value_idx = (values_per_thread * thread_idx +
leftovers_before_this_thread_idx);
S64 thread_opl_value_idx = thread_first_value_idx + values_per_thread;
if(thread_has_leftover)
{
thread_opl_value_idx += 1;
}Or more succinctly:
S64 values_per_thread = values_count / thread_count;
S64 leftover_values_count = values_count % thread_count;
B32 thread_has_leftover = (thread_idx < leftover_values_count);
S64 leftovers_before_this_thread_idx = (thread_has_leftover
? thread_idx
: leftover_values_count);
S64 thread_first_value_idx = (values_per_thread * thread_idx +
leftovers_before_this_thread_idx);
S64 thread_opl_value_idx = (thread_first_value_idx + values_per_thread +
!!thread_has_leftover);Now, using this [first, opl) calculation, we can arrange each thread to only loop over its associated range, thus not duplicating all sum work done by other threads.
2. Combining All Thread Sums
Now, how might we combine each thread’s sum to form the total sum? There are two simple options available: (a) we can define a global sum counter to which each thread atomically adds (using atomic add intrinsics) its per-thread sum, or (b) we can define global storage which stores all thread sums, and each thread can duplicate the work of computing the total sum.
For (a), we just need to define sum as static, and atomically add each thread_sum to it:
static S64 sum = 0;
void EntryPoint(void *params)
{
// ...
// compute `thread_sum`
// ...
AtomicAddEval64(&sum, thread_sum);
}Note: This has a downside in that only one thread group can be executing this codepath at once. This is sometimes not a practical concern, since if we are going wide at all, we are often using all available cores to do so, and it is likely not beneficial to also have some other thread group executing the same codepath for a different purpose. That said, it’s now a new hidden restriction of this code, and it can be a critical problem. There are some techniques we can use to solve this problem, which I will cover later—for now, the important concept is that the data is shared across participating threads.
For (b), we’d instead have a global table, and duplicate the work of summing across all thread sums. But we can only do that after we know that each thread has completed its summation work—otherwise we’d potentially add some other thread’s sum before it was actually computed!
static S64 thread_sums[NUMBER_OF_CORES] = {0};
void EntryPoint(void *params)
{
// ...
// compute `thread_sum`
// ...
thread_sums[thread_idx] = thread_sum;
// ??? need to wait here for all threads to finish!
S64 sum = 0;
for(S64 t_idx = 0; t_idx < NUMBER_OF_CORES; t_idx += 1)
{
sum += thread_sums[t_idx];
}
}That extra waiting requirement might seem like an argument in favor of (a), but we’d actually need the same mechanism if we did (a) once we wanted to actually use the sum—we’d need to wait for all threads to reach some point, so that we’d know that they’d all atomically updated sum.
We can use a barrier to do this. In (a):
static S64 sum = 0;
static Barrier barrier = {0};
void EntryPoint(void *params)
{
// ...
// compute `thread_sum`
// ...
AtomicAddEval64(&sum, thread_sum);
BarrierSync(barrier);
// `sum` is now fully computed!
}And in (b):
static S64 thread_sums[NUMBER_OF_CORES] = {0};
static Barrier barrier = {0};
void EntryPoint(void *params)
{
// ...
// compute `thread_sum`
// ...
thread_sums[thread_idx] = thread_sum;
BarrierSync(barrier);
S64 sum = 0;
for(S64 t_idx = 0; t_idx < NUMBER_OF_CORES; t_idx += 1)
{
sum += thread_sums[t_idx];
}
// `sum` is now fully computed!
}At this point, we have everything we need for both (a) and (b). Both are simple, and likely negligibly different. (a) requires atomic summation across all the threads, which implies hardware-level synchronization, whereas (b) duplicates the sum of all per-thread sums—these likely subtly differ in there costs, but not by much when compared to the actual values summation.
Going Narrow
Now, while I hope this summation example has been a useful introduction, I know it’s a bit contrived, and incomplete. Specifically, it’s missing two key parts of any program: inputs and outputs. What are we doing with this sum, and how do we use that in producing some form of output, and how do obtain the inputs, and store them in values and values_count?
Let’s barely extend the summation example with stories for the inputs and outputs. For the inputs, let’s say that we read values out of a binary file, which just contains the whole array stored as it will be in memory. For the outputs, let’s say that we just print the sum to stdout with printf.
Printing out the sum will be the easiest part, so let’s begin with that.
In single-core code, after computing the sum, we’d simply call printf:
S64 sum = ...;
// ...
printf("Sum: %I64d", sum);We can start by just doing the same in our “multi-core by default” code. What we’ll find is that our output looks something like this:
Sum: 12345678
Sum: 12345678
Sum: 12345678
Sum: 12345678
Sum: 12345678
Sum: 12345678
Sum: 12345678
Sum: 12345678And obviously, we only want our many cores to be involved with the majority of the computation, but we only need one thread to do the actual printf. In other words, we need to go narrow. Luckily, going narrow from wide code is much simpler than going wide from narrow code:
S64 sum = ...;
// ...
if(thread_idx == 0)
{
printf("Sum: %I64d", sum);
}We simply need to mask away the work from all threads except one.
Now, let’s consider the input problem. We need to compute values_count based on the size of some input file, allocate storage for values, and then fill values by reading all data from the file.
Single-threaded code to do that might look something like this:
char *input_path = ...;
File file = FileOpen(input_path);
S64 size = SizeFromFile(file);
S64 values_count = (size / sizeof(S64));
S64 *values = (S64 *)Allocate(values_count * sizeof(values[0]));
FileRead(file, 0, values_count * sizeof(values[0]), values);
FileClose(file);So, naturally, one option is to simply do this narrow:
if(thread_idx == 0)
{
char *input_path = ...;
File file = FileOpen(input_path);
S64 size = SizeFromFile(file);
S64 values_count = (size / sizeof(S64));
S64 *values = (S64 *)Allocate(values_count * sizeof(values[0]));
FileRead(file, 0, values_count * sizeof(values[0]), values);
FileClose(file);
}
BarrierSync(barrier); // `values` and `values_count` ready after this pointThis will work, but we somehow need to broadcast the computed values of values and values_count across all threads. One easy way to do this is simply to pull them out as static, like we did for shared data earlier:
static S64 values_count = 0;
static S64 *values = 0;
if(thread_idx == 0)
{
char *input_path = ...;
File file = FileOpen(input_path);
S64 size = SizeFromFile(file);
values_count = (size / sizeof(S64));
values = (S64 *)Allocate(values_count * sizeof(values[0]));
FileRead(file, 0, values_count * sizeof(values[0]), values);
FileClose(file);
}
BarrierSync(barrier);But consider that we might not want to do this completely single-core. It might be the case that it’s more efficient to issue FileReads from many threads, rather than just one. In practice, this is partly true (although, depending on the full stack—the kernel, the storage drive hardware, and so on—it may not be beneficial past some number of threads, and for certain read sizes).
So let’s say we’d like to do the FileReads wide now also. We need to still allocate values on a single thread, but once that is done, we can distribute the rest of the work trivially:
// we can open the file on all threads (though for some reasons
// we may want to deduplicate this too - for simplicity I am
// keeping it on all threads)
File file = FileOpen(input_path);
// calculate number of values and allocate (only single thread)
static S64 values_count = 0;
static S64 *values = 0;
if(thread_idx == 0)
{
S64 size = SizeFromFile(file);
values_count = (size / sizeof(S64));
values = (S64 *)Allocate(values_count * sizeof(values[0]));
}
BarrierSync(barrier);
// compute thread's range of values (same calculation as before)
S64 thread_first_value_idx = ...;
S64 thread_opl_value_idx = ...;
// do read of this thread's portion
S64 num_values_this_thread = (thread_opl_value_idx - thread_first_value_idx);
FileRead(file,
thread_first_value_idx*sizeof(values[0]),
num_values_this_thread*sizeof(values[0]),
values + thread_first_value_idx);
// close file on all threads
FileClose(file);It’s much simpler, now—compared to, say, the original parallel for case—to simply take another part of the problem like this, and to also distribute it amongst threads, simply because wide is the default shape of the program.
Instead of spending most programming time acting like we’re on a single-core machine, we simply assume our actual circumstances, which is that we have several cores, and sometimes we need to tie it all together with a few serial dependencies.
Non-Uniform Work Distributions
Let’s take a look at our earlier calculations to distribute portions of the values array:
S64 values_per_thread = values_count / thread_count;
S64 leftover_values_count = values_count % thread_count;
B32 thread_has_leftover = (thread_idx < leftover_values_count);
S64 leftovers_before_this_thread_idx = (thread_has_leftover
? thread_idx
: leftover_values_count);
S64 thread_first_value_idx = (values_per_thread * thread_idx +
leftovers_before_this_thread_idx);
S64 thread_opl_value_idx = (thread_first_value_idx + values_per_thread +
!!thread_has_leftover);This was an easy case, because uniformly dividing portions of values produces nearly uniform work across all cores.
If, in a different scenario, we don’t produce nearly uniform work across all cores, we have a problem: some cores will finish their work in some section long before others, and they’ll be stuck at the next barrier synchronization point while the other cores finish. This diminishes the returns we obtain from going wide in the first place.
Thus, it’s always important to uniformly distribute work whenever it’s possible. The exact strategy for doing so will vary by problem. But I’ve noticed three common strategies:
Uniformly distributing inputs produces uniformly distributed work (the case with the sum). So, we can decide the work distribution upfront.
Each portion of an input requires a variable amount of per-core work. The work is relatively bounded, and there are many portions of input (larger than the core count). So, we can dynamically grab work on each core, so cores which complete smaller work first receive more, whereas cores that are stuck on longer work leave more units of work for other cores.
Each portion of an input requires a variable amount of per-core work, but there is a small number (lower than the core count) of potentially very long sequences of work. We can attempt to redesign this algorithm such that it can be distributed more uniformly instead.
We’ve already covered the first strategy with the sum example—let’s look at the latter two.
Dynamically Assigning Many Variable-Work Tasks
Let’s consider a case where we have many units of work—“tasks”—and we’d like to distribute these tasks across cores. We may start by distributing the tasks in the same way that we distributed values to sum in the earlier example:
Task *tasks = ...;
S64 tasks_count = ...;
S64 thread_first_task_idx = ...;
S64 thread_opl_task_idx = ...;
for(S64 task_idx = thread_first_task_idx;
task_idx < thread_last_task_idx;
task_idx += 1)
{
// do task
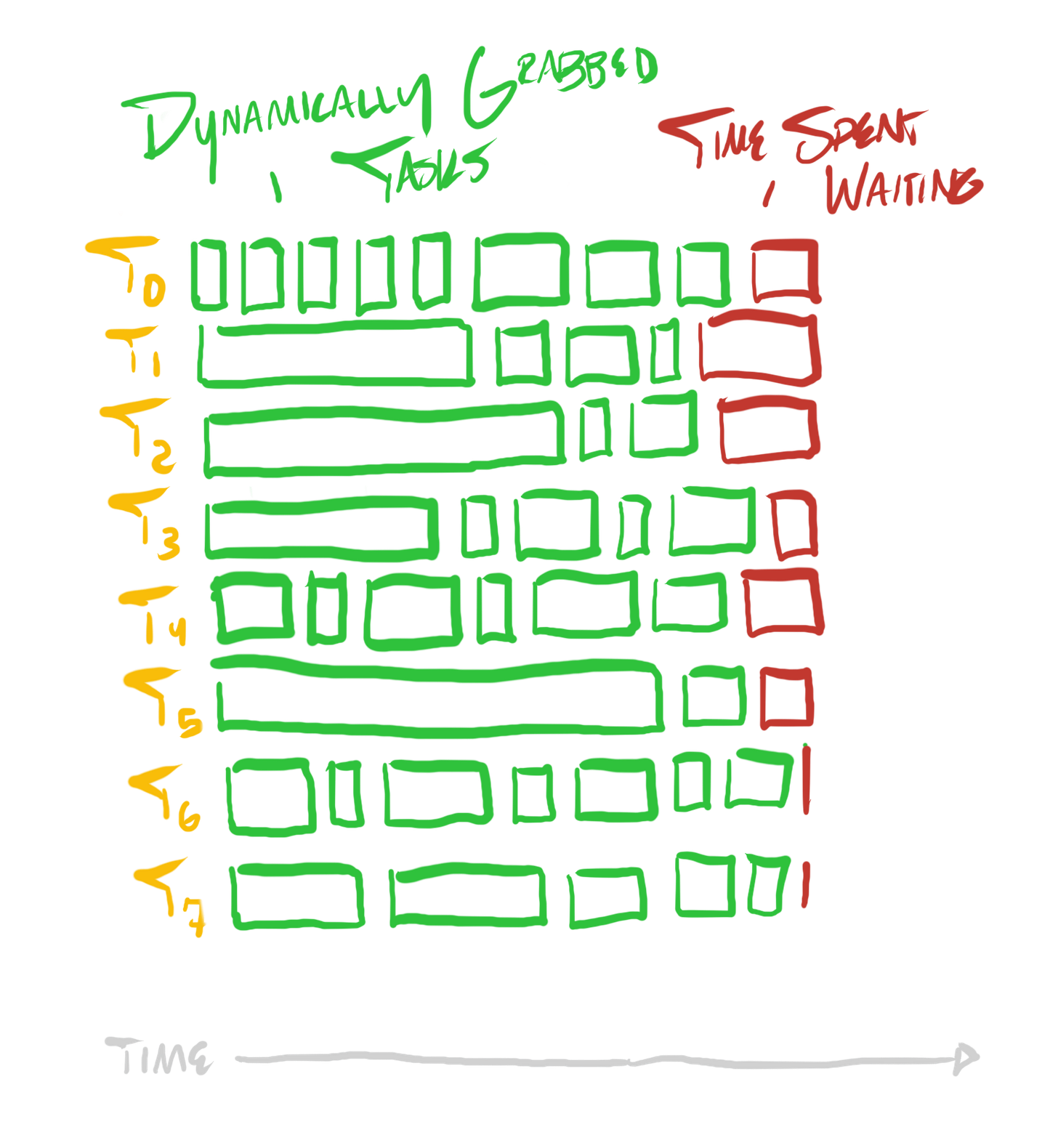
}If each task requires a variable amount of work, then a profile of the program might look something like this:
Instead of deciding the task division upfront, we can dynamically assign tasks, such that the threads which are occupied (performing larger tasks) are not assigned more tasks until they’re done, and threads which complete shorter tasks earlier are quickly assigned more tasks, if available.
We can do that simply with a shared atomic counter, which each thread increments:
Task *tasks = ...;
S64 tasks_count = ...;
// set up the counter
static S64 task_take_counter = 0;
task_take_counter = 0;
BarrierSync(barrirer);
// loop on all threads - take tasks as long as we can
for(;;)
{
S64 task_idx = AtomicIncEval64(&task_take_counter) - 1;
if(task_idx >= tasks_count)
{
break;
}
// do task
}This will dynamically distribute tasks across the cores, so that a profile of the program will look more like this:
Redesigning Algorithms For Uniform Work Distribution
Dynamically assigning tasks to cores will help in many cases, but it gets less effective if tasks are highly variable, to the point of sometimes being exceedingly long (e.g. many times more expensive than smaller tasks), or if there are fewer tasks than the number of cores.
In these cases, it can often be helpful to reconsider the serial independencies within a single task, or whether the same effect as a highly serially-dependent algorithm can be provided by an alternative highly serially-independent algorithm. Can a single task be subdivided further? Can it be performed in a different way? Can serially-dependent work be untangled from heavier work which can be done in a serially-independent way?
The answers to such questions are highly problem-specific, so it’s impossible to offer substantially more useful advice while staying similarly generic. But to illustrate that it’s sometimes possible—even when counterintuitive—I have an example problem from my recent work, in which finding more uniform work distribution required switching from a single-threaded comparison sort to a highly parallelizable radix sort.
In this problem, I had a small number of arrays that needed to be sorted, but these arrays were potentially very large, thus requiring a fairly expensive sorting pass.
My first approach was to simply distribute the comparison sort tasks themselves, so I would sort one array on a single core, while other cores would be sorting other arrays. But as I’ve said, there were a relatively small number of arrays, and the arrays were large, so sorting was fairly expensive—thus, most cores were doing nothing, and simply waiting for the small number of cores performing sorts to finish.
This approach would’ve worked fine if I had a larger number of smaller tasks. In fact, another part of the same program does distribute single-threaded comparison sort tasks in this way, because in that part of the problem, there are a larger number of smaller tasks.
In this case, I needed to sort array elements based on 64-bit integer keys. After sorting, the elements needed to be ordered such that their associated keys were ascending in value.
Conveniently, this can be done with a radix sort. I won’t cover the full details of the algorithm here (although I briefly covered it during a stream recently, which I recorded and uploaded here), but the important detail is that a radix sort requires a fixed number of O(N) passes over the array, and huge portions of work in each pass can be distributed uniformly across cores (in the same way that we distributed the sum work earlier).
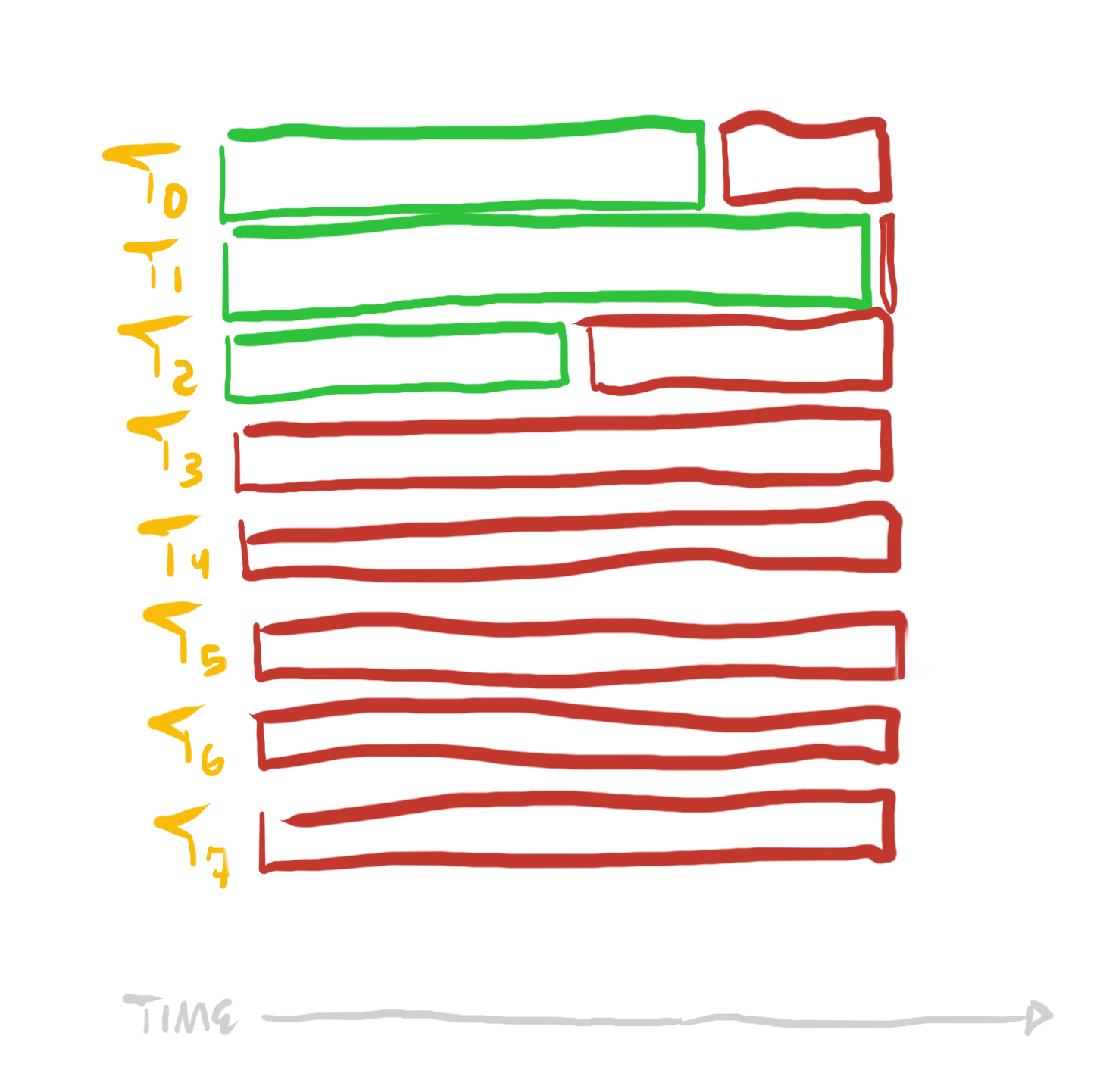
Now, all cores participate in every larger sorting task, but they only perform a nearly uniform fraction of the work in each sort. This results in a much more uniform work distribution, and thus a much shorter total time spend sorting:
This is just one concrete example a larger pattern I’ve noticed: In many problems, upon close examination, some serial dependencies can either vanish, or they can be untangled from heavier work.
In some problems, serially-dependent parts of the algorithm can be isolated, such that they prepare data which allows the rest of the algorithm to be done in a serially-independent fashion. Imagine a program which walks a linked list early, on a single core, to compute a layout in a serially-dependent way. This layout can then allow subsequent work to execute just using the full layout, rather than forcing that subsequent work to also include the serially-dependent pointer chasing.
Single-Threaded, Just Better
Code which is multi-core by default feels like normal single-threaded code, just with a few extra constructs that express the missing information needed to execute on multiple cores. This style has some useful and interesting properties, which make it preferable in many contexts to many of the popular styles of multi-core code found in the wild.
Single-Core as a Parameterization
One interesting implication of code written in this way—to be multi-core by default—is that it offers a strict superset of functionality than code which is written to be single-core, because “multi-core” in this case includes “single-core”, as one possible case. We can use the same code to execute on only a single core, simply by instead executing our entry point on a single thread, and parameterizing that thread with thread_idx = 0 and thread_count = 1.
In that case, one core necessarily receives all of the work. BarrierSyncs turn into no-ops, since there is only one thread (there are no other threads to wait for). Thus, it is equivalent to single-core functionality.
Simpler Debugging
This style of multi-core programming requires far less busywork and machinery in order to use multiple cores for some codepath. But one of the problems I mentioned with job systems and parallel fors earlier was not only that they require more busywork and machinery, but that they’re also more difficult to debug.
In this case, debugging is much simpler—in fact, it doesn’t look all that different from single-core debugging. At every point, you have access to a full call stack, and all contextual data which led to whatever point in time that you happen to be inspecting in a debugger.
Furthermore, because all threads involved are nearly homogeneous (rather than the generic job system, where all threads are heterogeneous at all times), debugging a single thread is a lot like debugging all threads. This is especially true because—between barrier synchronization points—the threads are all executing the same code. In other words, the context and state on one thread is likely to be highly informative of the context and state on all threads.
Access To The Full Stack
Because the context for some through line of computation frequently changes in traditional job systems, extra machinery must be involved to pipe data from one context to another—across jobs and threads—and maintain any associated allocations and lifetimes. But in this style, resources and lifetimes are kept as simple as they are in single-threaded code.
The stack, containing all contextual state at any point, becomes a single bucket for useful thread-local storage. In a job system, the stack is useful multi-core thread-local storage, but only for the duration of the job. The job is equivalent to the inner body of a for—this is a tiny, fragmentary scope. With this style, the entire stack is available, at any point.
Codebase Support
I’ve found some useful patterns which can be extracted and widely used in code which is multi-core by default. These patterns seem as widely applicable as arenas—as such, they can be a useful addition to a codebase’s base layer.
Thread-Local Group Data
LaneIdx(), LaneCount(), LaneSync()
The earlier example code frequently uses the thread_idx, thread_count, and barrier variables. Passing these to every codepath which might need them is redundant and cumbersome. As such, they are good candidates for thread-local storage.
In my code, I’ve bundled these into the base layer’s “thread context”, which is a thread-local structure which is universally accessible—it’s where, for example, thread-local scratch arenas are stored.
This provides all code the ability to read its index within a thread group (thread_idx), or the number of threads in its group (thread_count), and to synchronize with other lanes (BarrierSync).
As I suggested earlier, any code’s caller can choose “how wide”—how many cores—they’d like to execute that code, by configuring this per-thread storage. In general, shallow parts of a call stack can decide how wide deeper parts of a call stack are executed. If some work is expected to be small (to the point where it doesn’t benefit from being executed on many cores), and other cores can be doing other useful work, then before doing that work, the calling code can simply set thread_idx = 0, thread_count = 1, and barrier = {0}.
This means that a single thread may participate in many different thread groups—in other words, thread_idx and thread_count are not static within the execution of a single thread. Therefore, I found it appropriate to introduce another disambiguating term: lane. A lane is distinct from a thread in that a lane is simply one thread within a potentially-temporary group of threads, all executing the same code.
As such, in my terminology, thread_idx is exposed as LaneIdx(), and thread_count is exposed as LaneCount(). To synchronize with other lanes, a helper LaneSync() is available, which just waits on the thread context’s currently selected barrier.
Uniformly Distributing Ranges Amongst Lanes
LaneRange(count)
I’ve mentioned the following computation multiple times:
S64 values_per_thread = values_count / thread_count;
S64 leftover_values_count = values_count % thread_count;
B32 thread_has_leftover = (thread_idx < leftover_values_count);
S64 leftovers_before_this_thread_idx = (thread_has_leftover
? thread_idx
: leftover_values_count);
S64 thread_first_value_idx = (values_per_thread * thread_idx +
leftovers_before_this_thread_idx);
S64 thread_opl_value_idx = (thread_first_value_idx + values_per_thread +
!!thread_has_leftover);This is useful whenever a uniformly distributed range corresponds to uniformly distributed work amongst cores. As I mentioned, this is sometimes not desirable. But nevertheless, it’s an extremely common case. As such, I found it useful to expose this as LaneRange(count):
Rng1U64 range = LaneRange(count);
for(U64 idx = range.min; idx < range.max; idx += 1)
{
// ...
}Broadcasting Data Across Lanes
LaneSyncU64(value_ptr, source_lane_idx)
Earlier, we saw that when a variable needs to be shared across lanes, it can simply be marked as static. I mentioned that this has the unfortunate downside that only a single group can be executing the code at one time, since one group of lanes could trample over the static variable while another group is still using it. As I mentioned, this is sometimes not a concern (since it’s desirable to only have a single lane group executing some code), but it invisibly makes code inapplicable for some cases.
For example, let’s suppose I have some code which is written to be multi-core by default. Depending on the inputs to this codepath, I may want this to be executed—on the same inputs—with all of my cores. But in other cases, I may want this to be executed with only a single core—I may still want to execute this codepath on other cores, but for different inputs. That requires many lane groups to be executing the code at the same time, thus disqualifying the use of static to share data amongst lanes within the same group.
To address this, I also created a simple mechanism to broadcast small amounts of data across lanes.
Each thread context also stores—in addition to a lane index, lane count, and lane group barrier—a pointer to a shared buffer, which is the same value for all lanes in the same group.
If one lane has a value which it needs to be broadcasted to other lanes—for instance, if it allocated a buffer that the other lanes are about to fill—then that value can be communicated in the following way:
U64 broadcast_size = ...; // the number of bytes to broadcast
U64 broadcast_src_lane_idx = ...; // the index of the broadcasting lane
void *lane_local_storage = ...; // unique for each lane
void *lane_shared_storage = ...; // same for all lanes
// copy from broadcaster -> shared
if(LaneIdx() == broadcast_src_lane_idx)
{
MemoryCopy(lane_shared_storage, lane_local_storage, broadcast_size);
}
LaneSync();
// copy from shared -> broadcastees
if(LaneIdx() != broadcast_src_lane_idx)
{
MemoryCopy(lane_local_storage, lane_shared_storage, broadcast_size);
}
LaneSync();I’ve found that this shared buffer just needs to be big enough to broadcast 8 bytes, given that most small data can be broadcasted with a small number of 8 byte broadcasts, and larger data can be broadcasted with a single pointer broadcast.
I expose this mechanism with the following API:
U64 some_value = 0;
U64 src_lane_idx = 0;
LaneSyncU64(&some_value, src_lane_idx);
// after this line, all lanes share the same value for `some_value`It might be used in the following way:
// set `values_count`, allocate for `values`, on lane 0, then
// broadcast their values to all other lanes:
S64 values_count = 0;
S64 *values = 0;
if(LaneIdx() == 0)
{
values_count = ...;
values = Allocate(sizeof(values[0]) * values_count);
}
LaneSyncU64(&values_count, 0);
LaneSyncU64(&values, 0);Revisiting The Summation Example
With the above mechanisms, we can program the original summation example with the following steps.
First, we load the values from the file:
U64 values_count = 0;
S64 *values = 0;
{
File file = FileOpen(input_path);
values_count = SizeFromFile(file) / sizeof(values[0]);
if(LaneIdx() == 0)
{
values = (S64 *)Allocate(values_count * sizeof(values[0]));
}
LaneSyncU64(&values);
Rng1U64 value_range = LaneRange(values_count);
Rng1U64 byte_range = R1U64(value_range.min * sizeof(values[0]),
value_range.max * sizeof(values[0]));
FileRead(file, byte_range, values + value_range.min);
FileClose(file);
}
LaneSync();Then, we perform the sum across all lanes:
// grab the shared counter
S64 sum = 0;
S64 *sum_ptr = ∑
LaneSyncU64(&sum_ptr, 0);
// calculate lane's sum
S64 lane_sum = 0;
Rng1U64 range = LaneRange(values_count);
for(U64 idx = range.min; idx < range.max; idx += 1)
{
lane_sum += values[idx];
}
// contribute this lane's sum to the total sum
AtomicAddEval64(sum_ptr, lane_sum);
LaneSync();
LaneSyncU64(&sum, 0);And finally, we output the sum value:
if(LaneIdx() == 0)
{
printf(”Sum: %I64d\n”);
}Closing Thoughts
The concepts I’ve shared in this post represent what I feel is a fundamental shift in how CPU code can be expressed, compared to the normal single-core code all programmers are familiar with. Through small, additional annotations to code—basic concepts like LaneIdx(), LaneCount(), and LaneSync()—all code can contain the information necessary to be executed wide, using multiple cores to better take advantage of serial independence.
The same exact code can also be executed on a single core, meaning through these extra annotations, that code becomes strictly more flexible—at the low level—than its single-core equivalent which does not have these annotations.
Note that this is still not a comprehensive family of multithreading techniques, because it is strictly zooming in on one unique timeline of work, and how a single timeline can be accelerated using the fundamental multi-core reality of modern machines. But consider that programs often require multiple heterogeneous timelines of work, where one lane group is not in lockstep with others, and thus should not prohibit others from making progress.
But what I appreciate about the ideas in this post is that they do not unnecessarily introduce extra timelines. Communication between two heterogeneous timelines has intrinsic, relativity-related complexity. Those will always be necessary. But why pay that complexity cost everywhere, to accomplish simple multi-core execution?
I’m aware that, for many, these ideas are old news—indeed, everyone learns different things at different times. But in my own past programming, and when I look at the programming of many others, it seems that there is an awful lot of overengineering to do what seems trivial, and indeed what is trivial in other domains (like shader programming). So, for at least many people, these concepts do not seem well-known or old (even if they are in some circles and domains).
In any case, the concepts I’ve shared in this post have been dramatically helpful in improving my ability to structure multi-core code without overcomplication, and it seemed like an important-enough shift to carefully document it here.
I hope it was similarly helpful to you, if you didn’t know the concepts, or if you did, I hope it was nonetheless interesting.
If you enjoyed this post, please consider subscribing. Thanks for reading.
-Ryan






Great post, thank you for sharing. Do you intend on writing all or most of your future programs like this?
Also, I kinda wonder what would happen if hypothetically, every program running on a computer were written to allocate NUM_CORES_ON_MACHINE threads upfront and use this multicore by default approach. I would imagine that in 99% of normal home user scenarios where you really only care about one program (the one you are currently interacting with), it would be very beneficial. But maybe if for some reason you were running lots of individual processes at once and cared about how long it takes for all of them to complete at once, there might not be much different in the overall time taken...
In the context of a broader game engine design, how might this "CPU shader" approach be designed?
I think this may be one of those areas that as you mention at the end of the article may not fit 100% (and is in fact requiring heterogenous systems), but I'll try to flesh out the idea in a thought exercise.
In an ideal world, it seems like each thread would simply run their copy of the game loop. Thread 0 would probably be responsible for keeping time and gathering inputs (and maybe a barrier sync could be used if that's required), and then afterwards each thread pulls out relevant update tasks from its portion of the update queue (and propagates any tasks it'd like done at the end of its update section).
I think one problem with this approach tho is that components like OpenGL (or SDL iirc) lock themselves to the main thread, and require response from that thread to do anything. So you cant arbitrarily assign any thread to interact with those systems. That can be argued as an issue of engineering cruft.
A more fundamental issue may lie in things like the input and timekeeping code. For game logic, it seems like it'd be best to have a referee thread that acts as the source of truth. If multiple threads independently gather input or do timekeeping, that'd become messy very quickly.
Let me know your thoughts